Arquivos de Impressão: Tamanho A4.
Será que a mente pode ser explicado por um modelo matemático? Será que a matemática e o conhecimento humano é uma parte da mente? Muitos concordarão que a matemática é uma das realizações intelectuais da mente humana. Por este motivo cremos que se formalizarmos um modelo, que se equipare em generalidade ao sistema nervoso, a linguagem matemática estará incluída neste modelo.
Neste capítulo mostraremos que podemos fazer uma associação entre a teoria dos conjuntos e dos grafos com a do formalismo aqui definido que chamaremos de sistemas neural genérico. Neste formalismo os conjuntos de qualquer sistema matemático são associados aos "nós" ou neurônios de um sistema neural genérico. As funções que estabelecem relações entre os elementos dos conjuntos que são variáveis são representadas pelos "ramos" ou conexões inter-neurais do modelo. Estas relações podem ser determinísticas ou probabilísticas. O modelo pode ter uma representação em forma de lista ou de um grafo. O espaço de um sistema neural genérico será representado pelos possíveis estados de suas variáveis. O passar do tempo de nosso modelo é representado pelos movimentos, variações e mais precisamente iterações das funções do sistema. O espaço e o tempo físico como conhecemos é um caso particular dos espaços e tempos possíveis no nosso sistema neural genérico. Pois assim como a matemática, as teorias físicas também são uma realização e uma parte do pensamento humano. Quando definirmos claramente estas idéias mostraremos que a aprendizagem em um sistema matemático ocorre quando as funções do sistema variam com o tempo. Então apresentaremos a função de aprendizagem de vários modelos matemáticos tradicionais e concluiremos esta seção com a forma genérica da equação de aprendizagem.
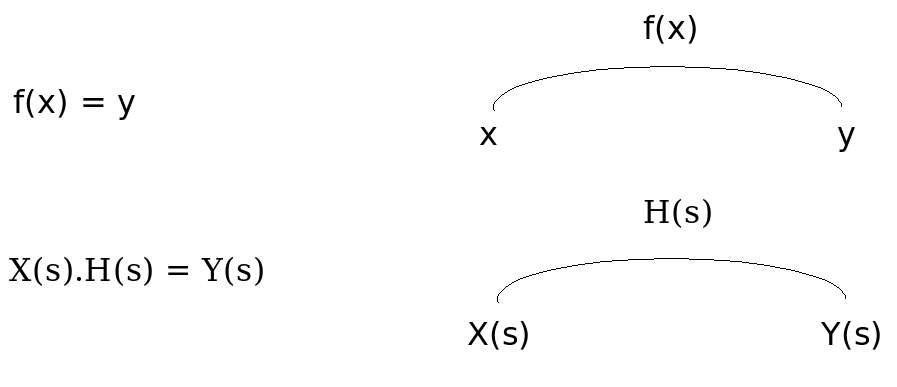
Uma das teorias mais fundamentais da matemática é a teoria dos conjuntos e de suas funções. Qualquer modelo matemático é composto de um conjunto de possibilidades e de funções relacionando os elementos variáveis destes conjuntos. Um sistema neural genérico é simplesmente um grafo onde os conjuntos de variáveis do sistema matemático são associados aos "neurônios" do sistema, e as funções que relacionam estes conjuntos são representadas pelas conexões destes. Seguem alguns exemplos de sistemas matemáticos representados pelos respectivos sistemas neurais genéricos.
Os computadores em certo sentido são mais próximos da mente humana que os modelos matemáticos. Se observarmos os computadores como um caso particular dos sistemas neurais genéricos os conjuntos de variáveis do modelo matemático representados pelos neurônios corresponde aos bits de informação da memória dos computadores. As funções do modelo matemático representadas pelas conexões do sistema neural genérico correspondem aos softwares dos computadores. Para falar da generalidade deste modelo podemos pensar nos computadores como um processador de símbolos e de informação. O matemático deve ser humilde para constatar que qualquer conhecimento matemático que tenha chegado a ele por meio da linguagem humana escrita ou falada, veio através de símbolos. Qualquer imagem ou informação que possa estar no computador cabe em um caso particular dos sistemas neurais genéricos. Basta pegar o modelo matemático ou seja apenas uma sequência de palavras ou seja lá o que for e colocar no computador. Feito isto associe a memória e os dados com os neurônios e as funções e programas com as conexões do sistema neural genérico. A denominação genérico, é necessária pois as redes neurais artificiais e o aspecto simbólico dos sistemas nervosos biológicos podem ser representados pelos sistemas neurais genéricos.
A generalidade do computador está no fato que ele é um processador de informações 62. E a generalidade disto está na amplitude e abrangência do conceito de quantidade de informação. A quantidade de informação de um evento em bits é o logatítimo na base dois do inverso da probabilidade de ocorrência deste evento. Um evento dentre outros pode ser sempre simbolizado como uma "letra" dentro de um alfabeto. Tudo para dizer que o conceito fundamental por trás dos sistemas neurais genéricos é a idéia de símbolo como definido na seção filosófica 2.3 deste trabalho. A probabilidade de existência dos símbolos determina a quantidade de informação. A quantidade de informação é o elemento da memória dos computadores onde estão não apenas os dados mas também os programas que os animam. Muitas das idéias matemáticas podem ser mapeadas em um computador. Os modelos matemáticos simbolizáveis pelas informações de uma linguagem humana, de um livro, de um desenho ou de um software de computador é um caso particular de um sistema neural genérico. Nestes sistemas os símbolos possíveis de existirem em variáveis quantidades são representados pelo estado dos nós neuronais de nosso sistema neural genérico. As relações funcionais e lógicas que dizem a respeito de como a existência destes símbolos ocorre e em que probabilidade, são representadas pelos ramificações que conectam os neurônios do nosso sistema neural genérico.
Se a atividade eletroquímica dos neurônios é dentre uma espécie de símbolo da realidade exterior e nós não podemos ter consciência direta, dos campos de força, das partículas e das substâncias essenciais que formam nosso próprio cérebro, então este modelo chamado sistema neural genérico é capaz não só de representar a matemática como também um aspecto de nossa mente. Os símbolos representados na atividade eletroquímica de nossos neurônios são modelados pelo estado dos neurônios artificiais de nosso sistema neural genérico. As conexões sinápticas que determinam as relações funcionais inter-neurais são modeladas pelas ramificações que conectam os neurônios artificiais de nosso sistema neural genérico.
Em um sistema neural genérico, o estado dos nós neuronais corresponde à um espaço de possibilidades e os movimentos das variáveis regulados pelas funções das conexões correspondem ao passar do tempo. A associação de espaço com estado e conjunto e de movimento com tempo e função, generaliza estes conceitos da física. No sistema neural genérico cada valor variável em cada nó neuronal corresponde à uma dimensão do espaço de estados. Por sua vez as funções características das ramificações que conectam os neurônios determinam como à cada iteração a cada diferencial as variáveis se movem e este movimento é o passar do tempo no sistema. Em certo sentido o espaço e o tempo físico são são o caso particular contínuo do espaço e tempo genérico definido acima para nosso sistema neural genérico. Com razão o leitor pode reclamar, porquê mais uma nomeclatura para os conjuntos e funções matemáticas? Por que chamar de sistemas neuronais genéricos, e não grafo genérico, a uma representação dos conjuntos e funções de um modelo matemático? O objetivo desta nomeclatura é simplesmente lembrar que os modelos simbólicos estão em nossa mente material. Mas também existe um objetivo mais amplo de generalização que consiste numa única estrutura simbólica encontrar uma linguagem flexível o suficiente para falar de qualquer modelo matemático. A representação gráfica é muito informativa. Nela também estará os fundamentos para se fazer um software de computador com paralelismo e em tempo real.
Os sistemas neurais genéricos enfatizam e representam graficamente conceitos abrangentes da matemática: conjuntos de elementos e funções. Estes conceitos matemáticas se relacionam com os fenômenos de espaço e tempo da física e com a idéia filosófica de elementos e movimentos. A teoria dos conjuntos e mais precisamente o Platonismo teórico dos conjuntos [set theoretical Platonism] é uma das escolas da matemática. Ela é exemplificada pelo matemático Kurt Gödel. Existem outras escolas de fundamentos da matemática63 como a formalista adotada por David Hilbert, a intuicionista exemplificada por L. E. J. Brouwer, e a logicista defendida por Bertrand Russell64.
Neste trabalho utilizaremos a teoria dos conjuntos para representar um sistema neural genérico. Cada neurônio é representado por um elemento de um conjuto. As conexões e relações causais entre os neurônios são representadas pelas funções.
Vamos agora definir um dos pré-requisitos para que haja aprendizagem em um sistema matemático. Como vimos um sistema neuronal genérico é um modelo de qualquer sistema matemático onde os conjuntos de elementos variáveis são representados pelos "nós" neuronais de um grafo e as funções são representadas pelos "ramos" que conectam os neurônios do grafo.
Uma função é definida como uma operação em um conjunto chamado domínio que computa o valor de um conjunto chamado imagem. O domínio é a causa lógica, a imagem é a consequência lógica e a operação é o movimento do sistema que determina o passar do "tempo" lógico do sistema neuronal genérico que pode também ser chamado de modelo matemático genérico. Com isso pretendemos dizer que entendemos por função uma operação sobre as causas que logicamente implicam em uma consequência. Isto significa que os grafos que representam os sistemas neuronais genéricos são grafos direcionais. Isto não impede que hajam realimentações e um conjunto domínio passe a ser imagem e vice versa através de um circuito de conexões. Agora imagine nosso sistema neuronal. Tudo que você imaginou são variáveis dentro do sistema, o que você não imaginou são variáveis fora do sistema. Como somos limitados você deve concordar comigo que os conjuntos de símbolos variáveis internos do sistema serão classificados como fazendo parte dele e os conjuntos de símbolos variáveis externos a ele serão classificados como o exterior do Sistema Neuronal Genérico (SNG). Definiremos as variáveis de entrada como sendo aquelas variáveis externas que fazem parte do domínio das funções de entrada do sistema e as variáveis de saída como sendo aquelas variáveis externas que fazem parte da imagem das funções de saída do sistema. A função de aprendizagem é uma função que a medida que o sistema opera modifica as funções do sistema.
A inteligência artificial é uma área de pesquisa multidisciplinar que objetiva realizar sistemas artificiais como o computador, que realizem tarefas típicas da inteligência do ser humano como por exemplo a linguagem, a percepção e o controle do meio ambiente. Uma "inteligência artificial" é uma inteligência que não aparece naturalmente e expontaneamente no meio ambiente. Uma "inteligência artificial" é feita e programada pelo ser humano. Talvez seja impossível um ser humano fazer artificialmente um sistema inteligente tão complexo quanto sua própria inteligência. Contudo existe uma alternativa que consiste em um ser humano fazer um sistema que aprenda com o meio ambiente. Este trabalho se entitula "Teoria da Aprendizagem", é sobre os sistemas que aprendem e que se tornam inteligentes naturalmente.
Alguns autores [45] observam dois enfoques nesta área de pesquisa denominada inteligência artificial. De um lado estão os simbolistas e de outro estão os conexionistas. Os simbolistas, como o nome diz, enfatizam principalmente os símbolos como aqueles das diferentes linguagens. Os conexionistas, por outro lado, buscam inspiração no sistema nervoso humano e simulam grosseiramente as suas conexões através de redes neurais artificiais. As redes neurais artificiais se modificam com o tempo e por isso constituem sistemas que aprendem e se adaptam. Contudo, não está muito claro para muitos o significado simbólico dos valores dos elementos de uma rede neural artificial. Neste capítulo mostraremos como é possível introduzir a noção de aprendizagem no formalismo matemático dos simbolistas e como é possível dar um significado simbólico ao estado dos neurônios de uma rede artificial. O resultado será um "casamento" das idéias destas duas visões.
Comecemos por formalizar simbolicamente a idéia de um sistema que aprende. Um sistema é definido matematicamente por um conjunto de elementos e funções que os relacionam. Um sistema que aprende seria um sistema que modificasse as funções matemáticas que o caracterizam. Assim como nós temos os sentidos, a mente e os músculos, os sistemas artificiais possuem os elementos de entrada, os elementos internos e os elementos de saída. Assim como nós temos a função cognitiva e a função motora, os sistemas artificiais possuem a função de entrada e a de saída.
Marvin Minsky (1972 [52]), um renomado pesquisador da área de inteligência artificial, cujo enfoque é mais simbolista do que conexionista, define um sistema digital de acordo com as seguintes equações:
O estado interno futuro é função do estado interno presente e das entradas de um sistema, ou seja,
| (6.1) |
Saídas futuras são função do estado interno presente e das entradas de um sistema
| (6.2) |
I = Input = Entradas do sistema (exemplo: uma câmara, microfone ou teclado de um computador)
S = Saída do sistema (exemplo: um monitor, uma caixa de som ou uma impressora de computador)
Fe = Função de entrada do sistema que determina um novo estado em função do estado anterior e das entradas
Fs = Função de saída do sistema que determina a saída em função do estado anterior e das entradas
n = um instante "n" qualquer do relógio do sistema digital
n + 1 = o instante seguinte ao instante "n"
O sistema digital acima é definido por um conjunto de elementos internos (E) e externos (I,S) e de funções (Fe, Fs) lógicas que relacionam estes elementos. Neste sistema, como na maioria dos outros, os elementos (E, I, S) que o formam, se relacionam e variam de acordo com as funções (Fe,Fs) características do sistema. Contudo as funções (Fe,Fs) são estáticas e não se modificam com o tempo. Num sistema que aprende estas funções se modificariam de acordo com as equações:
Funções do sistema são modificadas em função do conjunto de elementos e funções passadas do sistema
| (6.3) |
O exemplo anterior ilustra a idéia de que um sistema é caracterizado por um conjunto de elementos e funções. Nos sistemas convencionais os elementos internos e externos se modificam de acordo com as funções estáticas que caracterizam o sistema. Um sistema que aprende é um sistema no qual as funções que o caracterizam se modificam com o tempo. Vamos dar um outro exemplo ilustrativo desta idéia de aprendizagem. Alguns sistemas de controle podem ser definidos pelas seguintes equações de estado [58]:
A derivada das variáveis de estado função do valor delas e das entradas
As saídas do sistema são função do valor das variáveis de estado e das entradas
x = Vetor com as variáveis de estado do sistema
[dx/dt] = Derivada em relação ao tempo (t) do vetor de variáveis de estado (x)
u = Vetor com as entradas do sistema
y = Vetor com as saídas do sistema.
A, B, C, D = matrizes do sistema que determinam como as variáveis de estado (x) e as saídas (y) do sistema variam em função das variáveis de estado (x) e das entradas do sistema (u).
Repare que, como no caso digital, nós temos no caso analógico as funções características do sistema (A, B, C, D) que determinam a dinâmica dos elementos de quantidades variáveis internos (x) e externos (u, y) ao sistema. Embora o valor quantitativo dos elementos do sistema (x,y,u) variem, as matrizes (A, B, C, D) funcionais do sistema são estáticas no domínio das frequências. O conceito de aprendizagem definido como uma modificação das funções características do sistema (A, B, C, D) pode ser matematicamente definido neste caso de um sistema de controle analógico como sendo:
Funções do sistema são modificadas em função do conjunto de elementos e funções passadas do sistema
Fa = Função de aprendizagem que modificam as funções de entrada(A, B) e saída (C, D) do sistema, que por sua vez determinam como o valor dos elementos internos (x) e externos (y,u) variam.
Podemos fazer uma comparação deste sistema de controle analógico, com o sistema digital e até mesmo com o sistema nervoso humano. De acordo com os símbolos que utilizamos anteriormente para definir os elementos e funções do sistema digital e do sistema analógico observamos que:
| Função de aprendizagem em diferentes sistemas | |||
| Partes do sistema | Sistema Nervoso | Sistema Digital | Sistema Analógico |
| Entradas | Sentidos | I | u |
| Elementos internos | Cérebro | E | x |
| Saídas | Músculos | S | y |
| Função de Entrada | Função cognitiva | E(n+1) = Fe[E(n), I(n)] | dx/dt = A.x + B.u |
| Função de Saída | Função motora | S(n+1) = Fs[E(n), I(n)] | y = C.x + D.u |
| Função de Aprendizagem | Aprendizagem | [Fe, Fs] = Fa [Fe, Fs, E, I, S] | [A, B, C, D] = Fa [A, B, C, D , x, u] |
O leitor deve perceber o caminho que estamos seguindo. Definimos matematicamente os sistemas que aprendem como sendo aqueles cujas funções características se modificam de alguma forma com o tempo. Então aos poucos nós fomos ilustrando esta definição para sistemas cada vez mais genéricos. Primeiro um sistema digital e depois um sistema analógico. Vamos agora generalizar mais ainda estas idéias e aplica-las aos sistemas estudados na teoria dos circuitos [14]. Definiremos a noção de aprendizagem neste caso.
Os circuitos elétricos são representados por desenhos chamados grafos que indicam os caminhos por onde os elétrons circulam no circuito. Estes caminhos são chamados "Ramos da Rede [R]" elétrica. Os elétrons que entram (input = I) e caminham em cada ramo, são a corrente elétrica (I) daquele ramo. Os pontos de interconexão dos ramos do circuitos são chamados nós. O valor da Energia Elétrica (E) potencial em cada nó é a tensão elétrica do nó. Em geral existe uma relação matemática entre a corrente (I) que percorre um ramo, e a diferença de energia elétrica (E) potencial entre os dois nós extremos do ramo em questão. A forma matemática desta relação depende dos componentes contidos em cada ramo. Quando a diferença de Energia Elétrica Potencial entre o início e o fim de um ramo for diretamente proporcional a corrente no ramo (I), o componente é conhecido como resistor, quando for proporcional a integral, teremos um capacitor e quando for proporcional a derivada teremos um indutor. O fato é que definido com cuidado observamos em um circuito elétrico que:
| (6.4) |
I = Vetor de Corrente Elétrica em cada ramo do circuito.
R = Matriz diagonal do circuito que contém a geometria do circuito e a característica matemática dos componentes de cada ramo.
A matriz R contém tantas colunas quantos sejam os ramos do circuito, e tantas linhas quantos sejam os nós do circuito. Os elementos desta matriz são operadores matemáticos lineares, as vezes chamados de função de transferência do ramo ou mais tecnicamente a Transformada de Laplace da resposta em tensão de um ramo quando excitado por um impulso de corrente. O fato é que como no caso das matrizes (A,B,C e D) das equações de estado, a matriz [R] da rede é invariante no domínio das frequências. Isso significa que a função característica do sistema é a mesma. Para se introduzir o conceito de aprendizagem no caso dos circuitos elétricos, seria necessário algo do tipo:
| (6.5) |
Na verdade as equações acima se aplicam não apenas a circuitos elétricos, mas a inúmeros outros sistemas físicos. Seja em sistemas mecânicos lineares, ou angulares, seja em sistemas acústicos e outros sistemas físicos. Muitas vezes é possível definir uma grandeza física análoga a corrente elétrica e uma análoga a tensão elétrica, de tal forma que as duas multiplicadas resultem dimensionalmente na potência. A partir da definição das dimensões físicas da corrente e da tensão análoga, é possível definir a resistência, a indutância e a capacitância análoga. O fato é que os grafos podem ser usados para representar um grande número de sistemas físicos. Observe a tabela 6.11 de analogias, baseada na análise dimensional das várias grandezas físicas:
| Grandeza | Elétrica | Mecânica Linear | Mecânica Angular | Acústica |
onde: M = Massa, L = Espaço, T = Tempo
e Potência = Tensão x Carga = [(M ·L2)/(T3)]
Explicar como esta tabela é obtida, não é difícil. Pegue a grandeza física da primeira linha da tabela e chame-a de carga. Dividindo esta carga pelo tempo, você encontrará uma grandeza que mede a quantidade de carga que flui por um ramo do circuito entre dois nós em um intervalo de tempo. Chamaremos esta grandeza de corrente. Estes nomes estão entre aspas porque na verdade os nós do circuito correspondem a pontos do espaço com uma certa energia potencial. Os ramos do circuito correspondem a caminhos no espaço pelos quais flui a carga. E o fundamento destas analogias é a lei física da conservação de energia.
O fato é que a variação de energia potencial que ocorre quando a carga flui de um ponto do espaço para outro, tem que ser compensada por uma correspondente variação da energia cinética da carga. No final das contas uma certa quantidade de energia muda de forma por unidade de tempo. Energia dividida por tempo possui a dimensão da potência. Esta energia que muda da forma potencial para cinética quando as cargas caminham entre dois pontos do espaço com diferença de energia potencial, é exatamente a quantidade de carga que caminha nos ramos por unidade de tempo vezes a diferença de energia potencial entre os dois pontos do extremos do caminho. Se você observar com atenção a última frase verá que foi dito de uma outra forma que:
(Diferença de tensão entre os (nós) extremos do caminho (ramo)) × (corrente no caminho) = Potência.
(tensão) × (corrente) = Potência
A tensão e a corrente estão entre parênteses porque as suas dimensões físicas não são necessariamente de força e velocidade convencionais. Contudo se você olhar na tabela, verificará que a tensão é sempre a energia dividida pelo análogo da carga, e que a corrente é sempre esta carga dividida pelo tempo. Pode-se verificar também que em cada analogia a corrente vezes a tensão correspondente, sempre resulta dimensionalmente na potência. Em termos físicos o que acontece é que a potência é a força vezes a velocidade da carga. Cada tipo de carga responde a um tipo de campo de força diferente.
Se nos aprofundarmos no formalismo matemático da física clássica, iremos nos depararam com a lagrangiana de um sistema (Goldstein, 1980 [36]). A lagrangiana corresponde a energia total do sistema, cinética (movimento corrente) + potencial (tensão no espaço), sendo que a energia potencial e cinética, são dadas em função de grandezas genéricas. Para cada grandeza variável do sistema, é definida uma força específica que vezes a velocidade daquela grandeza resulta em potência. Desta forma conseguimos definir uma força genérica para cada unidade de espaço. A única coisa que tem que ser observada é que Força genérica vezes velocidade é igual a potência. No caso da mecânica linear esta equação é óbvia:
Força × deslocamento = Energia ⇒ Força × velocidade = Potência
No caso da mecânica angular teremos:
(Força angular) × ângulo = Torque × ângulo = Energia.
Como o ângulo em radianos é adimensional, as dimensões do torque devem ser a mesma da energia.
Agora ficou fácil de entender o princípio físico da conservação da energia pelo qual dimensionalmente as grandezas da tabela 6.11 de analogias foram formadas. Vamos aplica-los no caso dos circuitos elétricos.
| Grandeza | Elétrica |
| Carga | [(Carga2)/(distância2)] = Força ⇒ [(q2)/(L2)] = [(M ·L)/(T2)] ⇒ q2 = [(M ·L3)/(T2)] ⇒ q = [(√{M ·L3})/T] |
| Corrente [Carga/T] | [Carga/Tempo] = [q/T] = [([(√{M ·L3})/T])/T] = [(√{M ·L3})/(T2)] |
| Tensão [Potência/Corrente] | [([(Massa ·Espaço2)/(Tempo3)])/Corrente] = [([(M ·L2)/(T3)])/([(√{M ·L3})/(T2)])] = [(M ·L2)/(T ·√{M ·L3})] = [(√M ·L([4/2] − [3/2]))/T] = [(√{M ·L})/T] |
Vimos então um sistema digital, um sistema analógico e um sistema físico genérico representado por um grafo. A teoria dos circuitos, o conceito de grafos e de função de transferência, é talvez a representação gráfica e matemática mais genérica dos sistemas físicos que conheço. Contudo o conceito de grafo pode ser estendido para representar qualquer conjunto de elementos matemáticos e qualquer função, e não apenas os sistemas físicos que vimos anteriormente. De uma maneira simples uma variável matemática pode ser representada por um nó de um grafo, e uma função por um ramo. Quando falarmos sobre redes neurais artificiais, tornaremos mais exato o significado do conjunto de elementos do sistema representados pelos nós de um grafo e do conjunto de funções representado pelos ramos. Além disso daremos um exemplo de um sistema representado por uma rede neural artificial e detalharemos matematicamente a sua função de aprendizagem, antes disso porém gostaria de definir melhor o conceito de entrada e saída bem como dar um significado aos conjuntos de elementos e funções que definem um sistema. Tentarei explicar a seguinte tabela que usa o termo "elemento" e o termo "função" tão comuns a teoria dos conjuntos e a lógica matemática.
| Elementos do sistema | Funções do sistema |
| Elementos Internos (Ei) Conjunto de elementos variáveis internos ao sistema | Função interna (Fi), Ei = Fi(Ei) O valor "futuro" dos elementos internos (Ei) é função (Fi) do valor "presente" e "passado" destes elementos (Ei). |
| Elementos Externos de entrada (Ee) Conjunto de elementos variáveis do meio que envolve o sistema que são "causas funcionais" da variação dos elementos internos do sistema | Função de entrada (Fe) Ei = Fe(Ee) O valor "futuro" dos elementos internos (Ei) é também função (Fe) do valor "presente" e "passado" dos elementos externos de entrada (Ee) do sistema. |
| Elementos Externos de saída (Es) Conjunto de elementos variáveis do meio que envolve o sistema que são "consequências funcionais" do valor dos elementos internos do sistema | Função de saída (Fs) Es = Fs(Ei) O valor "futuro" dos elementos externos de saída (Es) é função (Fs) do valor "presente" e "passado" dos elementos internos (Ei) do sistema. |
O aspecto que desejo ressaltar nesta tabela é que matematicamente um sistema é definido por funções que relacionam conjuntos de elementos variáveis externos e internos ao sistema. O conceito de elemento é a base da teoria dos conjuntos. O conceito de função é o caminho dos raciocínios lógico-matemáticos. Assim como na linguagem temos sujeito e verbo, na matemática temos elementos e funções. O sujeito substantivo e os elementos possuem substância e existência real. Os verbos e as funções são um movimento do sujeito e dos elementos. Os elementos determinam uma forma no espaço. As funções determinam um movimento dos elementos no tempo.
Contudo uma função matemática possui um conjunto de elementos chamado domínio que são as "causas lógicas" e o passado do fenômeno que está sendo modelado matematicamente. Além do conjunto domínio uma função matemática possui um conjunto de elementos chamado imagem que são as "consequências" lógicas e a imagem futura do que ocorrerá se nossas premissas estiverem corretas. Estas palavras objetivam ressaltar a abrangência de uma definição de aprendizagem, como sendo uma modificação das funções que caracterizam um sistema. Tudo que é definido matematicamente como sendo um conjunto de elementos e funções matemáticas, pode usufruir desta definição de aprendizagem.
Eu diria que o problema de calcular os valores dos elementos variáveis de um sistema caracterizado por uma função, é um problema de análise matemática. Nos sistemas que aprendem, o objetivo é inverso. A partir da variação dos elementos internos e externos do meio no qual o sistema se insere, a função característica do sistema é "construída". Este problema é um problema de síntese matemática comum quando se faz projetos de engenharia. Na engenharia frequentemente sabemos para cada entrada as saídas que o sistema deve apresentar. Então projetamos um sistema que realize a função desejada. Nós sintetizamos a função do sistema. A diferença é que esta função é sintetizada pelo ser humano, e por isso trata-se de uma síntese artificial. Assim embora a construção e modificação da função de um sistema seja aprendizagem segundo a definição dada, trata-se de uma síntese artificial. O objetivo final deste trabalho é apresentar um sistema cujas funções são sintetizadas naturalmente de acordo com o meio no qual o sistema está inserido.
O melhor exemplo de um sistema que aprende, nos moldes que estamos definindo, está nas redes neurais artificiais. Nestas redes os pesos das conexões são constantemente alterados. Mas como dissemos antes, os pesos dos ramos representam as funções do sistema. Dissemos também que aprender significa alterar as funções do sistema. Sendo assim, uma rede que altera as funções nos ramos, representa um sistema que aprende. O que desejei mostrar, com a tabela de analogias físicas, é a amplitude do conceito de circuitos e o vasto número de sistemas que ele representa. Agora vou mostrar como uma rede ou diagrama pode representar qualquer conjunto de elementos e funções matemáticas que os relacionam. Desta forma se reforçará a abrangência da definição de aprendizagem dada anteriormente. De maneira genérica cada elemento de determinada natureza que existe em diferentes quantidades numéricas, é representado por um nó da rede, e cada função matemática é representada por um ramo.
O que desejo exemplificar com estas expressões matemáticas e os correspondentes grafos, é o fato de que uma definição matemática de um sistema pode ser representada por um grafo, ou circuito, ou diagrama ou rede, ou os objetos e morfemas da teoria das categorias, seja lá o nome que se dê, os elementos podem ser representados pelos nós de uma rede e as funções pelos ramos. Para equações de uma e inúmeras variáveis, operadores lineares e diferencias, na forma matricial ou não, existe sempre um grafo que pode representar matematicamente o sistema. Uma outra forma de perceber isto é constatar que muitos circuitos podem ser representados por grafos e pelas correspondentes expressões matriciais com funções de transferência e operadores. Isso é mais um indicativo de que para toda formulação algébrica e matricial existe uma representação gráfica. De forma genérica então, teremos para uma grande classe de sistemas definidos matematicamente, a correspondente rede que o representa. Usarei uma representação matricial genérica para os vários sistemas representáveis por uma rede, direi que:
| (6.6) |
onde, [R] representa os ramos de uma rede de um sistema.
Pode ser visto também como uma matriz do sistema com tantas colunas quantos sejam os ramos da rede e tantas linhas quantos sejam os nós da rede. Os componentes nos ramos podem representar qualquer função matemática entre os elementos nos nós extremos do ramo em questão. Os vetores E e I da expressão acima podem receber significados diferentes conforme o contexto e a tabela abaixo:
| Contexto | E | I |
| Inteligência Artificial (simbolistas) | Estados do sistema | Input - Entradas do sistema |
| Inteligência Artificial (conexionistas) | Valor calculado pela função de ativação de um neurônio de uma rede neural artificial. | Valor nas conexões de uma rede neural que é igual a entrada vezes o peso da conexão. |
| Inteligência Natural (neurobiologistas) | Valor do potencial eletroquímico na membrana celular do corpo de um neurônio. | Número de pulsos por segundo nos axônios de um neurônio. |
| Engenharia Elétrica | Tensão nos nós do circuito | Corrente nos ramos do circuito |
| Física | Energia potencial nos pontos do espaço | Cargas genéricas que se movem, alterando sua energia cinética no tempo. |
| Engenharia de Comunicação | Energia | Informação |
| Matemática | Elementos do conjunto domínio nos n nós de um grafo, ou se preferir nas n dimensões de um espaço Rn. | Valor numérico da imagem de uma função matemática representada pelos ramos de um grafo matemático. |
| Genérico | Grandeza nos nós da rede [R] | Grandeza dos ramos da rede. |
De forma genérica então teremos uma função de aprendizagem dada por:
| (6.7) |
Assim de forma genérica os conjuntos matemáticos de elementos internos e externos de um sistema são representados pelos nós de uma rede de ramos [R]. E estes ramos da rede [R] correspondem às funções que caracterizam o sistema. Em muitos sistemas artificiais, normalmente as funções são fixas no tempo ou na frequência, e nós realizamos uma análise a partir destas funções estáticas a respeito da variação dos elementos imagem e domínio destas funções que são as grandezas variáveis do sistema. Nestes sistemas não existe aprendizagem, pois as funções do sistema, representadas pela matriz de ramos da rede [R], são estáticas no tempo ou na frequência. Esse contudo, não é o caso das redes neurais artificiais. Nestas redes as funções que relacionam os diversos elementos internos e externos do sistema, estão representadas nos valores dos pesos das conexões. Estes valores se alteram com o tempo. Conforme as entradas e saídas desejadas de uma rede neural artificial, a função característica do sistema na matriz de ramos da rede [R] se modifica. Uma rede neural artificial é o melhor exemplo da função de aprendizagem em um sistema artificial. Esta primeira parte deste trabalho, apenas mostrou como outros formalismos das funções matemáticas podem ser biunivocamente relacionados com um grafo, ou rede de ramos [R] se preferir. Sabendo que nos grafos as funções são representadas pelas operações que ocorrem nos ramos, fica fácil aplicar a definição de aprendizagem para qualquer sistema, qual seja, um sistema que aprende é aquele que modifica as suas funções características, que numa representação gráfico-matemática aparecem nos ramos da rede [R].
Concluímos aqui a parte matemática deste trabalho entitulada: "Teoria da Aprendizagem". Como havia prometido, nós demos uma definição matemática do que seria aprendizagem de um sistema.