Índice Superior Vai para o próximo: Capítulo 30
Arquivos de Impressão: Tamanho A4.
Em todos os tempos, no ensino da Lógica, a grande dor de cabeça dos alunos foram sempre os juízos modais.
Distinguiam os escolásticos quatro tipos de modais: possibilidade, contingência, impossibilidade e necessidade.
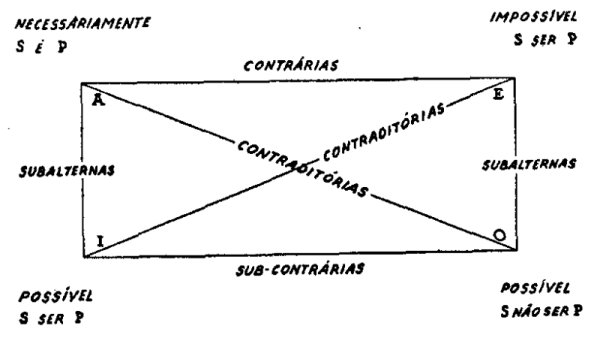
Aproveitando o famoso paralelogramo A, E, I, O, construíram-se os seguintes juízos:

Nas mesmas condições nestas proposições complexas, que contêm os advérbios do espaço e do tempo.
E - Nunca é ... (Sempre não é:) Em nenhum lugar é (aqui não é ...)
I - Algumas vezes é ... Em algum lugar é ...
O - Nem sempre é (alguma vez não é ...) Não é num lugar certo (não está em algum lugar ...)
O modo de necessidade equivale a uma proposição universal afirmativa; o modo impossibilidade, a uma proposição universal negativa, os modos de possibilidade e de contingência a proposições particulares, afirmativas ou negativas.
Deste modo, as proposições modais entram na classe dos juízos opostos, e permitem realizar conclusões.
A necessidade e a impossibilidade são contrárias.
A possibilidade positiva e a possibilidade negativa são sub-contrárias.
A necessidade e a possibilidade são subordinadas.
O mesmo se dá quanto à impossibilidade e à possibilidade negativa.
A necessidade e a possibilidade negativa são contraditórias.
Tomás de Aquino chamava a atenção para o carácter engenhoso das proposições modais, como também pela conveniência e o valor que as mesmas ofereciam à ciência. Modernamente, em face das grandes dificuldades que oferecem certas conclusões lógicos actuais têm apenas se cingido a conservar a regra a conservar a regra de que as conclusões modais, que se implicam, são subordinadas, e as que se excluem são contrárias ou contraditórias. Afirma-se o que segue: a necessidade implica a realidade, e a realidade implica a possibilidade; a impossibilidade exclui tanto a possibilidade, como a realidade e a necessidade. Se se conclui que uma lei da natureza é necessária, conclui-se que é ela real. Se ela deve ser, ela é, se ela é, é que ela é possível. Do que é impossível, conclui-se, portanto, que não é real; e se não é real não é necessário.
Por isso, alguns consideram a necessidade como uma espécie da realidade, e a realidade uma espécie da possibilidade, representada por três círculos concêntricos. Assim tudo quanto é necessário é real, tudo quanto é real, é possível.
Fora do círculo da possibilidade está a impossibilidade, que exclui, conseqüentemente, tudo quanto a possibilidade encerra.
Daí sobrevêm a fortiori as seguintes conclusões:
Da necessidade, conclui-se a realidade e a possibilidade.
Da realidade, conclui-se a possibilidade.
Da impossibilidade, concluem-se a não-realidade e a não-necessidade.
Da não-realidade, conclui-se a não-necessidade.
Contudo, as recíprocas não se concluem.
Da possibilidade não se conclui a realidade e a necessidade.
Da realidade, não se conclui a necessidade.
Da não-necessidade não se conclui a não realidade e a não-possibilidade.
Da não-realidade não se conclui a não-possibilidade.
No terreno das proposições modais, penetra-se, portanto, no campo da Metafísica, e aqui já há diversas maneiras de conceber as conclusões que acima apontamos. Alguns perguntam: pode-se, da necessidade, concluir a possibilidade? O que é necessário lògicamente é necessàriamente possível? Se se concebe como possível o que tem viabilidade de ser, é concludente que o necessário é possível, porque não se lhe poderia negar a viabilidade de ser.
Se o necessário exige o possível, o possível não exige o necessário.
Ninguém pode duvidar que possamos, da realidade, concluir a possibilidade. Contudo, como concluir, da possibilidade, a realidade? Sem dúvida, está aqui um dos pontos chaves da Metafísica, e que resolvido favoravelmente tornaria suficientemente apodítico o argumento ontológico de Santo Anselmo.
Podem-se colocar duas maneiras de considerar a possibilidade: a possibilidade de ser um contingente, a de um ser cuja não existência ou cuja não realidade fora de suas causas não seria contraditória, e a do ser, cuja não realidade acarretaria contradição. Assim, por exemplo, é possível não existir o ser contingente A, pois a sua não existência não acarreta contradição. Mas, considerado em função de outros sêres que existem, a sua não-existência tornaria impossível compreendê-los. Neste caso, sua necessidade é hipotética. Assim poder-se-ia concluir que entre os planêtas não pode haver um vazio absoluto devido às influências verificáveis entre os planêtas de um sistema e os sistemas entre si. A possibilidade de existência ou não de algo intermédio impunha-se por uma necessidade hipotética, ou seja em função necessária de outros modos de ser. Resta saber agora o que se poderia dizer em relação a uma necessidade absoluta. Assim, se a realidade e a existência do que há exige ou não a presença de um ser primeiro, fonte de todos os outros. Que um ser primeiro seja fonte de todos os outros é possível para a nossa maneira de conceber. A sua não-existência acarretaria a impossibilidade de explicação da existência dos sêres contingentes, porque êstes não têm em si a razão suficiente remotíssima de ser, como o provamos em Filosofia Concreta. A possibilidade de um ser absolutamente necessário é evidente. Se alcançarmos a sua possibilidade lógica, desta apenas não podemos concluir a necessidade absoluta. Contudo, a impossibilidade de explicar as coisas contingentes, sem a necessidade de ser um ser primeiro anterior a todas as coisas, e fonte e origem destas (Deus, matéria, energia, o nome pouco importa), é necessidade absoluta para a compreensão do mundo. Que se conclui daí? Conclui-se que a possibilidade da necessidade hipotética é a que decorre da relatividade funcional, mas a necessidade absoluta decorre da necessidade da explicação ontológica dos sêres contingentes. Pois bem, são nessas razões, ou subentendendo-as, que a prova ontológica encontra a sua validez apodítica9.