Índice Superior Vai para o próximo: Capítulo 24
Arquivos de Impressão: Tamanho A4.
Muitos são os filósofos que combatem o silogismo. Contudo, nenhum dêstes sabia usá-lo devidamente.
1) Aristóteles definia-o "como um enunciado no qual, tendo-se proposto algumas coisas, decorre delas, necessariamente, outra coisa, pelo só facto de serem dadas." Desta forma, o silogismo não diz mais do que já foi dito, não conclui mais do que já está contido numa das premissas. Ora, o silogismo é um raciocínio que vai do geral ao particular, portanto o que está contido na conclusão já está na premissa. Não oferece nenhum valor inventivo, mas apenas expositivo. Não se iguala à análise baseada no processo matemático, como já argumentava Descartes, ao combatê-lo.
2) Afirmam ainda outros que o silogismo não é uma forma natural do nosso pensar, mas sim artificial, porque, na realidade, não pensamos silogìsticamente.
Tais argumentos, em que pesem as razões de seus expositores, são improcedentes de certo modo.
Sabiam os antigos que o silogismo, não é espontâneo no homem, mas uma realização culta, superior, e a única capaz de assegurar raciocínios legítimos, seguros, portanto. Todo saber culto do homem funda-se nêles e sôbre êles e por meio dêles realiza suas mais profundas especulações.
Realmente, podemos reduzir todos os silogismos a algumas regras bem simples.
Já vimos as regras clássicas que são 8, e que encerram tudo quanto é necessário para que se tenha um silogismo rigoroso.
O princípio fundamental dos silogismos pode em parte ser reduzido ao axioma de que "duas coisas idênticas a uma terceira são idênticas entre si". Realmente o silogismo é um raciocínio deductivo, no qual se comparam dois extremos com um terceiro.
Mas, apesar de sua simplicidade, poucos, raríssimos, são os filósofos que sabem raciocinar bem e não ofendem essas regras elementares.
Por simples que sejam as regras clássicas práticas do silogismo, que são dadas também em versos latinos, houve sempre, entre os lógicos, o intuito de reduzi-las a uma única regra.
Vamos dar algumas das mais famosas. Balmes apresenta esta: "O princípio fundamental dos silogismos simples é o seguinte: as coisas idênticas a uma terceira são idênticas entre si." Funda-se assim no princípio de não-contradição: "é impossível que uma coisa seja e não seja ao mesmo tempo."
A conclusão está sempre contida nas premissas, e, portanto, afirmada implìcitamente numa delas.
A Lógica de Port-Royal dá esta regra, que logo nos indica a verdade ou a falsidade de um silogismo: "Uma das duas proposições deve conter a conclusão; a outra fazer ver que a contém."
Notem bem o sentido quantitativo desta regra, que é exacta, pois realmente toda conclusão é deduzida, é tirada. Todo silogismo serve para tirar de uma premissa, uma conclusão.
Veja-se esta regra de Euler: "Tudo o que existe no continente existe no conteúdo. Tudo o que está fora do continente está fora do conteúdo."
Observe-se o sentido puramente quantitativo dessa regra, que também é exacta.
Há ainda esta outra: "O que pode ser afirmado ou negado de todo um gênero, pode ser também afirmado ou negado de todos os indivíduos que compõem êsse gênero."
O gênero tem as notas gerais, as notas que se encontram em todos os indivíduos. A nota negada ao gênero é negada ao indivíduo.
Essa regra serve muito bem para o silogismo perfeito de Aristóteles, que já estudamos.
Quantitativamente, o que afirmamos do todo, afirmamos da parte. Não podemos tirar de um todo o que não está contido neste todo (Regra de Euler). Desta forma o que se conclui é deduzido de uma das proposições (regra de Port-Royal).
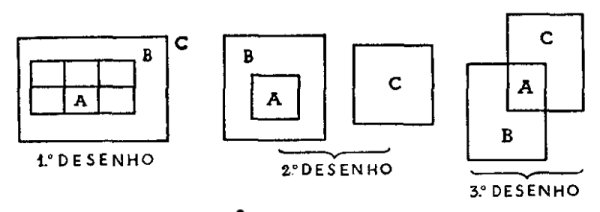
Euler, em suas "Cartas a uma princesa da Alemanha", expôs um método muito interessante, representando por círculos os três têrmos do silogismo. Com êsses círculos, que formam 36 figuras, examinou todas as espécies de silogismo.
Não vamos reproduzi-las, mas podemos reduzi-las a 3 figuras apenas, que são suficientes para responder às combinações legítimas que se podem formar dos silogismos. Simplificamos, assim, graficamente, o que tem sido um dos maiores problemas para os estudantes.
1) Ou um todo (com suas partes) está incluído noutro;
2) ou não está (e, neste caso, suas partes também não estão);
3) ou apenas parte do primeiro participa do outro.
São as três situações quantitativamente possíveis, nas quais, simplificadamente, se inclui qualquer silogismo. O que afirmamos do todo, afirmamos da parte. O que afirmamos do primeiro todo, negamos do segundo, quer em parte, quer no todo, se admitimos que êsse todo está à parte do primeiro. Se parte de um todo está contido em outro, o que afirmamos do primeiro todo, pode não estar contido no outro, pois admitimos que apenas parte é que está.

São, assim, os três desenhos que, graficamente, nos mostram todas as combinações legítimas possíveis.
Vejamos, agora, as combinações que podem ser comparadas com os desenhos:
ora, todo A é B; 1o desenho - Barbara
ora, todo A é B; 2o desenho - Celarent
algum C é A; 3o desenho - Darii
ora, algum A é B; 2o desenho - Ferio
ora, todo A é B; 2o desenho - Cesare
ora, nenhum C é B; 2o desenho - Camestres
ora, algum A é B; 2o desenho - Festino
ora, algum C não é B; 2o desenho - Baroco
ora, todo A é C; 1o desenho - Darapti
ora, todo A é B; 2o desenho - Felapton
ora, todo A é B; 3o desenho - Disamis
ora, algum A é C; 3o desenho - Datisi
ora, todo A é B; 2o desenho - Bocardo
ora, algum A é B; 2o desenho - Ferison
ora, todo B é C; 1o desenho - Bamalip
ora, nenhum B é C; 2o desenho - Calemes
ora, todo A é B; 3o desenho - Dimatis
ora, todo A é B; 2o desenho - Fesapo
ora, algum A é B; 2o desenho - Ferison
ora, todo A é B; 1o desenho - Baralipton
ora, todo A é B; 2o desenho - Celantes
ora, algum C é A; 3o desenho - Dabitis
ora, nenhum C é A; 2o desenho - Fapesmo
ora, nenhum C é A; 2o desenho - Friseso (morum)
Em suma: ou um todo está contido em outro; ou um todo está fora do outro; ou parte de um todo está contido em outro.
Dentro dessas três situações quantitativas, acham-se todos os silogismos rigorosos.
E daí se pode concluir: se uma coisa está contida em outra, o que se afirma da segunda se afirma da primeira. Se uma coisa não está contida em outra, o que se afirma da primeira não se afirma da segunda. Se ambas participam de uma parte, só há afirmação para ambas quanto à parte participada. O que se afirma do restante, que não é a parte participada, não se afirma da outra.
Todo silogismo é um raciocínio deductivo. Não se pode tirar de uma coisa, o que a coisa não tem. Assim duas coisas podem ser inteiramente iguais entre si, ou inteiramente diferentes, ou em parte se assemelharem. Assim duas idéias: ou são iguais ou totalmente diferentes ou em algo se assemelham.
Todo silogismo regular cinge-se a estas regras que repetimos de várias maneiras para melhor fixá-las na memória do leitor.