Arquivos de Impressão: Tamanho A4 (pdf), Tamanho A5 (pdf), Texto (txt).
Quando precisar use os seguintes valores para as constantes:
Considere um corpo esférico de raio r totalmente envolvido por um fluido de viscosidade η com velocidade média v. De acordo com a lei de Stokes, para baixas velocidades, esse corpo sofrerá a ação de uma força de arrasto viscoso dada por F = −6 πr ηv. A dimensão de η é dada por
| [η] = M L−1 T−1 |
| μ[η] = kg . m−1 s−1 |
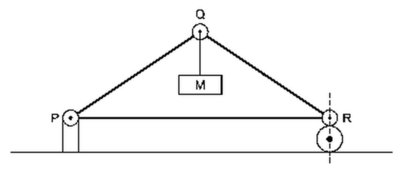
Três barras de peso desprezível, articuladas nos pinos P, Q e R, constituem uma estrutura vertical em forma de triângulo isósceles com 6,0 m de base e 4,0 m de altura, que sustenta uma massa M suspensa em Q em equilíbrio estático. O pino P também é articulado no seu apoio fixo, e o pino R apoia-se verticalmente sobre o rolete livre.

Sendo de 1,5 ×104 N e 5,0 ×103 N os respectivos valores máximos das forças de tração e compressão suportáveis por qualquer das barras, o máximo valor possível para M é de
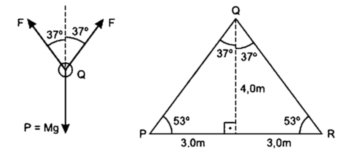
2F→ . 0,80 = M . 10 ⇒F→ = [ 10M/ 1,6] (SI)
2) A barra [PQ] está sendo comprimida pela força de intensidade F→:
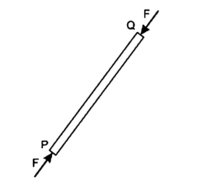
F→máx = [( 10M1)/ 1,6] = 5,0 . 103
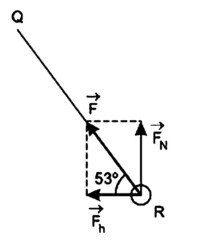
A força resultante entre a força normal F→N e a força F→h aplicada na haste [PR] deve ser igual à força de compressão F→ aplicada na haste [RQ].
| F→h = [ 6,0M/ 1,6] (SI) |
A haste [PR] estará sendo tracionada pela força de intensidade F→h:

F→máx = [( 6,0M2)/ 1,6] = 1,5 . 104 (SI)
| M2 = 4,0 . 103 kg |
Para que nenhuma das barras se rompa, devemos usar o menor valor entre M1 e M2:
| Mmáx = 8,0 . 102 kg |
No sistema de sinalização de trânsito urbano chamado de "onda verde", há semáforos com dispositivos eletrônicos que indicam a velocidade a ser mantida pelo motorista para alcançar o próximo sinal ainda aberto. Considere que de início o painel indique uma velocidade de 45 km/h. Alguns segundos depois ela passa para 50 km/h e, finalmente, para 60 km/h. Sabendo que a indicação de 50 km/h no painel demora 8,0 s antes de mudar para 60 km/h, então a distância entre os semáforos é de
Consideremos dois semáforos, S1 e S2, separados por uma distância D.
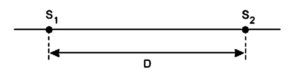
Um primeiro carro, A, passa por S1 e deverá manter uma velocidade escalar de 45km/h para pegar S2 aberto, gastando um tempo T1.
Um segundo carro, B, passa por S1 e deverá manter uma velocidade escalar de 50km/h para pegar S2 aberto, gastando um tempo T2.
D = [ 45/ 3,6] . T1 = [ 50/ 3,6] . T2
T1 = [ 3,6D/ 45] e T2 = [ 3,6D/ 50]
[ 3,6D/ 45] − [ 3,6D/ 50] = 8,0 (SI)
| D = 1,0km |
Um bloco de massa m encontra-se inicialmente em repouso sobre uma plataforma apoiada por uma mola, como visto na figura.
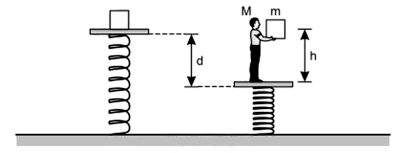
Em seguida, uma pessoa de massa M sobe na plataforma e ergue o bloco até uma altura h da plataforma, sendo que esta se desloca para baixo até uma distância d. Quando o bloco é solto das mãos, o sistema (plataforma + pessoa + mola) começa a oscilar e, ao fim da primeira oscilação completa, o bloco colide com a superfície da plataforma num choque totalmente inelástico. A razão entre a amplitude da primeira oscilação e a da que se segue após o choque é igual a
1) O acréscimo de deformação da mola é provocado pelo peso da pessoa:
| ⇒ k = [ Mg/ d] |
Quando m é abandonada, a aceleração adquirida pela pessoa é dada por:
| a = [ m g/ M] |
Esta aceleração é a aceleração máxima do MHS (Movimento Harmônico Simples) e é dada por:
a = amáx = [ m g/ M] = ω2 A1 (1)
Por outro lado: k = M ω2 ⇒ [ M g/ d] = M ω2
| ω2 = [ g/ d] (2) |
Substituindo-se (2) em (1), vem:
| ⇒ A1 = [ m d/ M] |
3) A velocidade do bloco m no instante da colisão é dada por:
V12 = 0 + 2 g h ⇒ V1 = √{2 g h}
4) No instante da colisão, a plataforma completou sua oscilação e voltou ao repouso. Usando a conservação da quantidade de movimento:
5) A nova posição de equilíbrio corresponde à posição da plataforma no instante em que o bloco m foi abandonado e portanto V2 será a velocidade máxima do novo MHS.
6) A nova pulsação será dada por:
ω12 = [ k/( M + m)] ⇒ ω1 = √{[ k/( M + m)]}
7) A nova amplitude de oscilação A2 é dada por:
[ m/( M + m)] √{2 g h} = √{[ k/( M + m)] A2}
A2 = [( m √{2 g h})/( M + m)] √{[( M + m)/ k]}
| A2 = [ m/( M + m)] √{[( 2 g h (M + m))/ k]} |
A2 = [ m/( M + m)] √{[( 2 g h (M + m))/( [ M g/ d])]}
A2 = [ m/( M + m)] √{[( 2 d h (M + m))/ M]}
[( A1)/( A2)] = [ m d/ M] . [( M + m)/ m] √{[ M/( 2 d h (M + m))]}
[( A1)/( A2)] = [( (M + m) d)/ M] √{[ M/( 2 d h (M + m))]}
[( A1)/( A2)] = √{[( (M + m))/ M] [ d/ 2 h]}
A partir do repouso, um foguete de brinquedo é lançado verticalmente do chão, mantendo uma aceleração constante de 5,00 m/s2 durante os 10,0 primeiros segundos. Desprezando a resistência do ar, a altura máxima atingida pelo foguete e o tempo total de sua permanência no ar são, respectivamente, de
1) Cálculo da altura após 10,0s:
H = 0 + 0 + [ 5,00/ 2] . 100 (m)
| ⇒ H1 = 250m |
2) Cálculo da velocidade escalar após 10,0s:
| ⇒ V1 = 50,0m/s |
3) Cálculo da altura máxima atingida:
0 = 2500 + 2 (−10,0) (Hmáx − 250)
| Hmáx = 375m |
4) Cálculo do tempo sob ação da gravidade:
T1 = [( 10,0 ± √{100 + 200})/ 2] (s)
| T1 ≅ 13,7s |
| ⇒ T = 23,7s |
Um caminhão baú de 2,00m de largura e centro de gravidade a 3,00m de chão percorre um trecho de estrada em curva com 76,8m de raio. Para manter a estabilidade do veículo neste trecho, sem derrapar, sua velocidade não deve exceder a
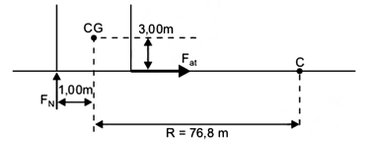
1) Na iminência de tombamento, o somatório dos torques em relação ao CG é nulo:
| Fat = [ 10m/ 3,00] |
2) A força de atrito faz o papel de resultante centrípeta:
[ 10m/ 3,00] = [( m V2)/ 76,8]
| ⇒ V = 16,0m/s |
Considere duas estrelas de um sistema binário em que cada qual descreve uma órbita circular em torno do centro de massa comum. Sobre tal sistema são feitas as seguintes afirmações:
I. O período de revolução é o mesmo para as duas estrelas.
II. Esse período é função apenas da constante gravitacional, da massa total do sistema e da distância entre ambas as estrelas.
III. Sendo R1 e R2 os vetores posição que unem o centro de massa do sistema aos respectivos centros de massa das estrelas, tanto R1 como R2 varrem áreas de mesma magnitude num mesmo intervalo de tempo.
Assinale a alternativa correta.
I) (V) As estrelas estão sempre alinhadas com o centro de massa e portanto terão a mesma velocidade angular e o mesmo período de translação.

1) Posição do centro de massa:
R1 = [( M . 0 + m . (R1 + R2))/( M + m)]
| R1 = [ m d/( M + m)] |
[ G M m/( d2)] = M . ω2 . [ m d/( M + m)]
ω2 = [( G (M + m))/( d3)] = ( [( 2 π)/ T] )2
[( 4 π2)/( T2)] = [( G (M + m))/( d3)]
T2 = [( 4 π2 d3)/( G (M + m))]
| ⇒ T = 2 π√{[( d3)/( G (M + m))]} |
T só depende de G, de (M + m) e de d.
Para o mesmo intervalo de tempo, o vetor posição de módulo maior varre área maior.
Um cubo de peso P1, construído com um material cuja densidade é ρ1, dispõe de uma região vazia em seu interior e, quando inteiramente imerso em um líquido de densidade ρ2, seu peso reduz-se a P2. Assinale a expressão com o volume da região vazia deste cubo.
| V = [( P1 − P2)/( ρ2 g)] |
| V1 = [( P1)/( ρ1 g)] |
3) Cálculo do volume da parte vazia:
| V0 = [( P1 − P2)/( ρ2 g)] − [( P1)/( ρ1 g)] |
Um pêndulo simples é composto por uma massa presa a um fio metálico de peso desprezível. A figura registra medidas do tempo T em segundos, para 10 oscilações completas e seguidas do pêndulo ocorridas ao longo das horas do dia, t.
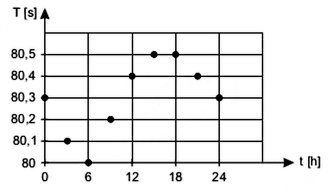
Considerando que neste dia houve uma variação térmica total de 20oC, assinale o valor do coeficiente de dilatação térmica do fio deste pêndulo.
Vamos considerar na resolução que o trecho do enunciado que diz "considerando que neste dia houve uma variação térmica total de 20oC" refira-se à máxima diferença de temperaturas verificada nesse dia, o que ocorreu entre 6h e 18h, segue-se que:
| T2 − T1 = 5,0 . 10−2s (1) |
⇒ T2 = 2 π√{[( L1 (1 + α∆θ))/ g]}
Logo: [( T2)/( T1)] = [( 2 π√{[( L1 (1 + α∆θ))/ g]})/( 2 π√{[( L1)/ g]})]
| T2 = √{1 + α20} . T1 (2) |
(III) (2) em (1) e lembrando-se de que
√{1 + α20} . T1 − T1 = 5,0 . 10−2
T1 (√{1 + α20} − 1) = 5,0 . 10−2
8,0 (√{1 + α20} − 1) = 5,0 . 10−2
Um pêndulo simples oscila com uma amplitude máxima de 60o em relação à vertical, momento em que a tensão no cabo é de 10 N. Assinale a opção com o valor da tensão no ponto em que ele atinge sua velocidade máxima.
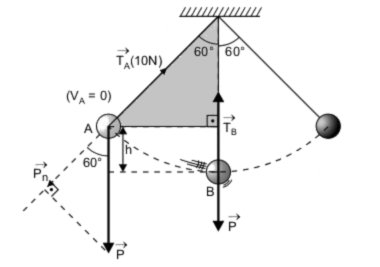
| h = [ L/ 2] |
II) A resultante centrípeta no ponto A é nula, já que a velocidade nesse ponto é nula. Logo:
Pn = TA ⇒ P cos60o = TA ⇒ P . [ 1/ 2] = 10
III) Conservação de energia mecânica:
[( m VB2)/ 2] = m g h ⇒ m VB2 = 2 P [ L/ 2]
| ⇒ m VB2 = 20 L |
IV) O ponto B é o local da trajetória em que a velocidade tem intensidade máxima. Em B:
TB − P = [( m VB2)/ L] ⇒ T − 20 = [ 20 L/ L]
| ⇒ T = 40 N |
Um líquido condutor (metal fundido) flui no interior de duas chapas metálicas paralelas, interdistantes de 2,0 cm, formando um capacitor plano, conforme a figura. Toda essa região interna está submetida a um campo homogêneo de indução magnética de 0,01 T, paralelo aos planos das chapas, atuando perpendicularmente à direção da velocidade do escoamento.
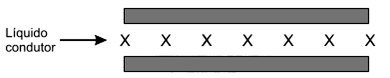
Assinale a opção com o módulo dessa velocidade quando a diferença de potencial medida entre as placas for de 0,40 mV.
Vamos supor que o líquido condutor contenha partículas eletrizadas que estejam deslocando-se com a mesma velocidade de escoamento do fluido.
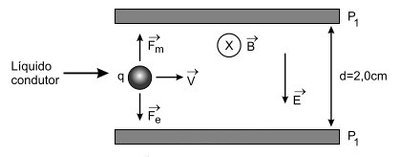
O movimento das partículas é retilíneo e uniforme. Assim, a força magnética e a força elétrica se equilibram.
1. Cálculo do módulo do campo elétrico entre as placas P1 e P2:
E = [ U/ d] = [( 4,0 . 10−4 V)/( 2,0 . 10−2 m)] ⇒ E = 2,0 . 10−2 V/m
2. Cálculo do módulo da velocidade:
V = [ E/ B] ⇒ V = [( 2,0 . 10−2)/( 1,0 . 10−2)] (m/s)
| V = 2,0 m/s |
Um estudante usa um tubo de Pitot esquematizado na figura para medir a velocidade do ar em um túnel de vento. A densidade do ar é igual a 1,2 kg/m3 e a densidade do líquido é 1,2 ×104 kg/m3, sendo h = 10 cm.
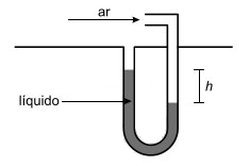
Nessas condições a velocidade do ar é aproximadamente igual a
A pressão hidrostática do líquido é equilibrada pela pressão dinâmica do ar:
1,2 . 104 . 10 . 0,10 = [ 1,2/ 2] Var2
| Var = 1,4 . 102 m/s |
Balão com gás Hélio inicialmente a 27oC de temperatura e pressão de 1,0 atm, a mesma do ar externo, sobe até o topo de uma montanha, quando o gás se resfria a −23oC e sua pressão reduz-se a 0,33 de atm, também a mesma do ar externo. Considerando invariável a aceleração da gravidade na subida, a razão entre as forças de empuxo que atuam no balão nestas duas posições é
Da Equação de Clapeyron, obtemos a densidade μ do ar no alto da montanha.
pV = [ m/ M] RT (M = massa molar média do ar)
De forma análoga, a densidade inicial μ0 do ar é dada por:
A intensidade E da força de empuxo sobre o balão é dada por:
E0 = [( M p0)/( R T0)] V0 g (2)
Dividindo a equação (1) pela equação (2), temos:
[ E/( E0)] = [( [ M p V/ R T] g)/( [( M p0 V0)/( R T0)] g)]
[ E/( E0)] = [( [ p V/ T])/( [( p0 V0)/( T0)])]
Da equação geral dos gases perfeitos, temos:
Um corpo flutua estavelmente em um tanque contendo dois líquidos imiscíveis, um com o dobro da densidade do outro, de tal forma que as interfaces líquido/líquido e líquido/ar dividem o volume do corpo exatamente em três partes iguais. Sendo completamente removido o líquido mais leve, qual proporção do volume do corpo permanece imerso no líquido restante?
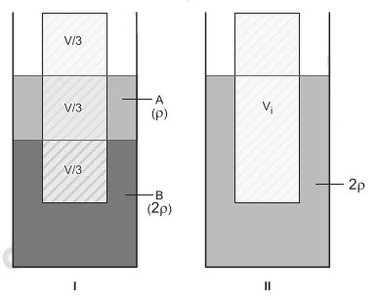
| Vi = [ V/ 2] |
A figura mostra uma placa fina de peso P dobrada em ângulo reto e disposta sobre uma esfera fixa de raio a.
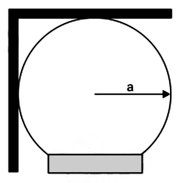
O coeficiente de atrito mínimo entre estes objetos para que a placa não escorregue é
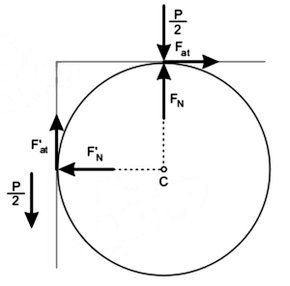
1) Condição de força resultante nula:
2) Condição de torque nulo em relação ao ponto C:
[ P/ 2] . R = F′at . R + Fat . R
[ (1)/ (2)] : [( μ+ [ 1/( μ)])/( μ+ 1)] = 2
μ2 + 1 = 2 μ2 + 2 μ⇒ μ2 + 2 μ− 1 = 0
μ = [( −2 ± √{4 + 4})/ 2] ⇒ μ = [( −2 + 2 √2)/ 2]
| μ = √2 − 1 |
Obs.: Admitindo-se que a barra foi dobrada ao meio.
Uma corda de cobre, com seção de raio rC, está submetida a uma tensão T. Uma corda de ferro, com seção de raio rF, de mesmo comprimento e emitindo ondas de mesma frequência que a do cobre, está submetida a uma tensão T/3. Sendo de 1,15 a razão entre as densidades do cobre e do ferro, e sabendo que ambas oscilam no modo fundamental, a razão rC/rF é igual a
(I) A frequência fundamental f de uma corda cilíndrica de comprimento L e raio r, submetida a uma força de tração T, é calculada pela Equação de Lagrange-Helmholtz.
f = [ 1/ 2 L] √{[ T/( ρ)]} (1)
Em que ρ é a densidade linear da corda ( ρ = [ m/ L] ).
(II) Sendo μ a densidade volumétrica da corda, supostamente referida no enunciado, tem-se:
μ = [ m/ Vol] = [ m/( πr2 L)] ⇒ μ = [( ρ)/( πr2)]
[ 1/( 2 LC)] √{[( TC)/( πμC rC2)]} = [ 1/( 2 LF)] √{[( TF)/( πμF rF2)]}
Sendo LC = LF, TC = T, TF = [ T/ 3] e
[( μC)/( μF)] = 1,15 ou μC = 1,15 μF, vem:
[ T/( 1,15 μF rC2)] = [ T/( 3 μF rF2)] ⇒ ( [( rC)/( rF)] )2 = [ 3/ 1,15]
| [( rC)/( rF)] ≅ 1,6 |
Um tubo de fibra óptica é basicamente um cilindro longo e transparente, de diâmetro d e índice de refração n. Se o tubo é curvado, parte dos raios de luz pode escapar e não se refletir na superfície interna do tubo.
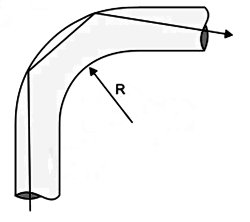
Para que haja reflexão total de um feixe de luz inicialmente paralelo ao eixo do tubo, o menor raio de curvatura interno R (ver figura) deve ser igual a
O esquema refere-se à situação de maior possibilidade de emergência do raio de luz da fibra óptica para o ar.
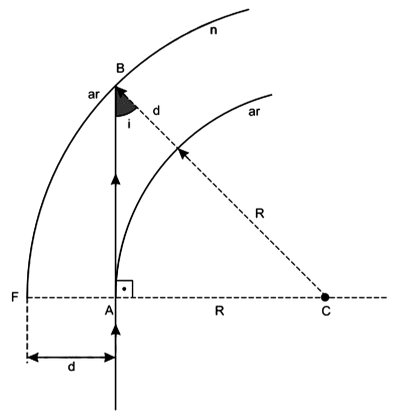
O seno do ângulo limite L para o dioptro fibra-ar é dado por:
A menor incidência interna na face FB da fibra ocorre para o raio de luz que se propaga sobre a reta [AB]. Do triângulo ABC, temos:
Para que ocorra reflexão total em B, a condição é i > L.
| R > [ d/( (n − 1))] |
No circuito da figura há três capacitores iguais, com C = 1 000 μF, inicialmente descarregados. Com as chaves (2) abertas e as chaves (1) fechadas, os capacitores são carregados. Na sequência, com as chaves (1) abertas e as chaves (2) fechadas, os capacitores são novamente descarregados e o processo se repete.
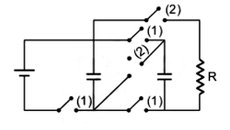
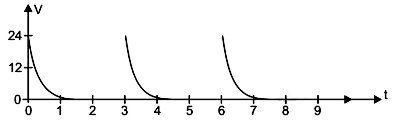
Com a tensão no resistor R variando segundo o gráfico da figura, a carga transferida pelos capacitores em cada descarga é igual a
1. Com as duas chaves (1) fechadas e as chaves (2) abertas, os capacitores se carregam como mostra o circuito a seguir (fig 1).
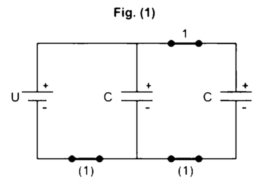
2. Fechando-se as duas chaves (2) e abrindo-se as três chaves (1), os capacitores mantêm a sua carga elétrica o novo circuito está mostrado na figura a seguir:
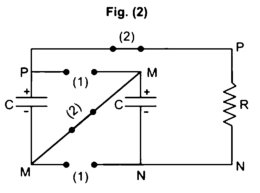
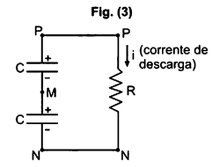
Os dois capacitores idênticos, de capacitância C, em série, têm uma capacitância equivalente igual a C/2. Sendo Q a carga de cada um deles, a associação tem uma carga total igual a Q. Portanto:
| Q = 1,2 . 10−2C |
Uma bobina metálica circular de raio r, com N espiras e resistência elétrica R, é atravessada por um campo de indução magnética de intensidade B. Se o raio da bobina é aumentado de uma fração ∆r << r, num intervalo de tempo ∆t, e desconsiderando as perdas, a máxima corrente induzida será de
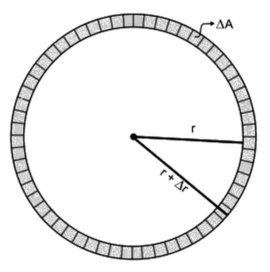
A corrente elétrica irá surgir nessa bobina devido à variação da área ∆A que é atravessada pelo campo magnético, assim:
1. Cálculo da variação da área ∆A.
∆A = π(r2 + 2 r ∆r + ∆r2) − πr2
∆A = πr2 + π2 r ∆r + π∆r2 − πr2
∆A = π2 r ∆r, pois ∆r2 pode ser desprezado.
2. Na situação de máxima variação de fluxo (∆Φ), temos:
3. O módulo da força eletromotriz induzida E será dado por:
| i = [( 2 πN B r ∆r)/( R ∆t)] |
Enquanto em repouso relativo a uma estrela, um astronauta vê a luz dela como predominantemente vermelha, de comprimento de onda próximo a 600nm. Acelerando sua nave na direção da estrela, a luz será vista como predominantemente violeta, de comprimento de onda próximo a 400nm, ocasião em que a razão da velocidade da nave em relação à da luz será de
Para o Efeito Doppler relativístico, temos:
[ 1/( λobs)] = √{[( 1 ± β)/( 1 ± β)]} . [ 1/( λfonte)]
na qual β é a razão entre o módulo da velocidade do observador (V) e o módulo de velocidade da luz (c):
No caso em que obsevador e fonte se aproximam, temos:
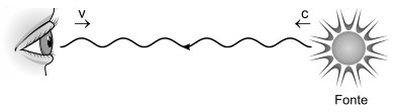
[ 1/( λobs)] = √{[( 1 + β)/( 1 − β)]} . [ 1/( λfonte)]
[ 1/ 400] = √{[( 1 + β)/( 1 − β)]} . [ 1/ 600]
[ 3/ 2] = √{[( 1 + β)/( 1 − β)]}
| β = [ 5/ 13] |
As questões dissertativas, numeradas de 21 a 30, devem ser desenvolvidas, justificadas e respondidas no caderno de soluções
No circuito abaixo os medidores de corrente e tensão elétrica são reais, ou seja, possuem resistência interna. Sabendo-se que o voltímetro acusa 3,0 V e o amperímetro, 0,8 A, calcule o valor da resistência interna do voltímetro.
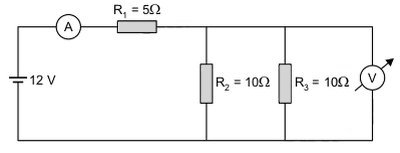
Esquematizando o circuito, temos:
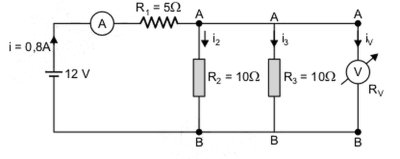
Mas i2 = i3, pois R2 e R3 têm valores iguais.
A intensidade total da corrente elétrica (i) pode ser determinada por:
0,8 = 0,3 + 0,3 + iv ⇒ iv = 0,2A
| Rv = 15 Ω |
No tráfego, um veículo deve se manter a uma distância segura do que vai logo à frente. Há países que adotam a "regra dos três segundos", vale dizer: ao observar que o veículo da frente passa por uma dada referência ao lado da pista, que se encontra a uma distância d, o motorista deverá passar por essa mesma referência somente após pelo menos três segundos, mantida constante sua velocidade v0. Nessas condições,
1. supondo que o veículo da frente pare instantaneamente, estando o de trás a uma distância ainda segura de acordo com a "regra dos três segundos", calcule o tempo T da frenagem deste para que ele possa percorrer essa distância d, mantida constante a aceleração.
2. para situações com diferentes valores da velocidade inicial v0, esboce um gráfico do módulo da aceleração do veículo de trás em função dessa velocidade, com o veículo parando completamente no intervalo de tempo T determinado no item anterior.
3. considerando que a aceleração a depende principalmente do coeficiente de atrito μ entre os pneus e o asfalto, explique como utilizar o gráfico para obter o valor máximo da velocidade vM para o qual a "regra dos três segundos" permanece válida. Sendo μ = 0,6 obtenha este valor.
A distância d deve ser percorrida com velocidade de módulo V0 em 3s. Portanto:
1) Usando a equação da velocidade escalar média:
[( ∆s)/( ∆t)] = [( V0 + Vf)/ 2]
[ d/ T] = [( V0 + 0)/ 2] ⇒ [( 3 V0)/ T] = [( V0)/ 2]
0 = V0 − a . 6,0 ⇒ a = [( V0)/ 6,0] (SI)
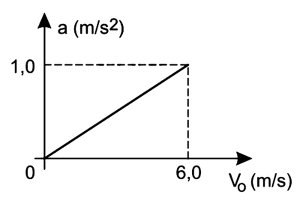
| ⇒ a = μg = 6,0 m/s2 |
Um cilindro vertical de seção reta de área A1, fechado, contendo gás e água é posto sobre um carrinho que pode se movimentar horizontalmente sem atrito. A uma profundidade h do cilindro, há um pequeno orifício de área A2 por onde escoa a água. Num certo instante a pressão do gás é p, a massa da água, Ma e a massa restante do sistema, M. Determine a aceleração do carrinho nesse instante mencionado em função dos parâmetros dados. Justifique as aproximações eventualmente realizadas.
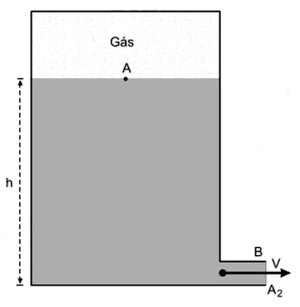
1) Aplicando-se a Equação de Bernoulli entre A e B, vem:
PA + [( μVa2)/ 2] + μg h = patm + [( μV2)/ 2]
Nota: admitimos que o orifício será feito próximo ao fundo do recipiente e vamos considerar Va ≅ 0.
| V2 = [( 2 (p − patm))/( μ)] + 2 g h (1) |
[( ∆m)/( ∆t)] = μA2 [( ∆x)/( ∆t)], em que [( ∆x)/( ∆t)] = V
F = [( ∆m)/( ∆t)] . V = μA2 V . V
| F = μA2 V2 |
a = ( [( μA2)/( Ma + M)] ) V2 (2)
a = ( [( μA2)/( Ma + M)] ) [ [( 2 (p − patm))/( μ)] + 2 g h ]
a = [( μA2)/( Ma + M)] [( 2 (p − patm + μg h))/( μ)]
| a = [( 2 A2 (p − patm + μg h))/( Ma + M)] |
O enunciado não citou a pressão atmosférica (patm), a densidade da água (μ) e o módulo g da aceleração da gravidade. Aproximações feitas:
1) O nível da água mantém-se horizontal.
2) O orifício próximo ao fundo do recipiente.
3) Velocidade nula na superfície da água.
Um dado instrumento, emitindo um único som de frequência f0, é solto no instante t = 0 de uma altura h em relação ao chão onde você, imóvel, mede a frequência f que a cada instante chega aos seus ouvidos. O gráfico resultante de [ 1/ f] ×t mostra uma reta de coeficiente angular −3,00 ×10−5. Desprezando a resistência do ar, determine o valor da frequência f0.
Gráfico qualitativo do fenômeno
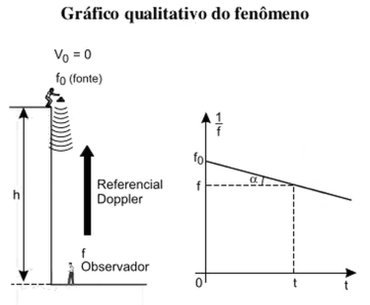
Equação do Efeito Doppler sonoro:
[ f/( Vsom + Vobservador)] = [( f0)/( Vsom − Vfonte)]
[ f/( 340 + 0)] = [( f0)/( 340 − 10 t)]
f = [( 340 f0)/( 340 − 10 t)] ⇒ [ 1/ f] = [ 1/( f0)] − [ t/( 34 f0)]
O coeficiente angular (a) da reta (tanα no gráfico da figura) corresponde a:
a = [ 1/( 34 f0)] ⇒ f0 = [ 1/ 34 a]
Sendo a = 3,00 . 10−5 (unidades SI), vem:
f0 = [ 1/( 34 . 3,00 . 10−5)] (Hz)
| f0 ≅ 980,4 Hz |
Resposta: Aproximadamente 980,4 Hz
Dois garotos com patins de rodinhas idênticos encontram-se numa superfície horizontal com atrito e, graças a uma interação, conseguem obter a razão entre seus respectivos pesos valendo-se apenas de uma fita métrica. Como é resolvida essa questão e quais os conceitos físicos envolvidos?
Representação do contexto proposto:
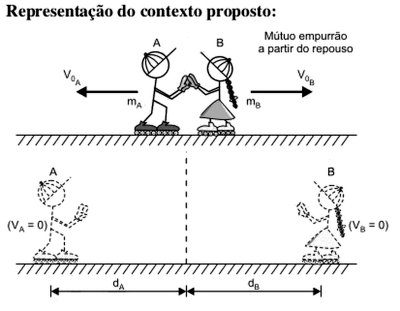
(I) Teorema da energia cinética:
τ = [( m V2)/ 2] − [( m V02)/ 2] ⇒ − Fat d = − [( m V02)/ 2]
| ⇒ V0 = √{2 μC g d} (1) |
(II) Conservação da quantidade de movimento no ato do mútuo empurrão:
Q→f = Q→i ⇒Q→A +Q→B = 0→ ⇒Q→A = −Q→B
Em módulo: QA = QB ⇒ mA VA = mB VB
mA g VA = mB g VB ⇒ PA VA = PB VB
| [( PA)/( PB)] = [( VB)/( VA)] (2) |
(III) Substituindo-se (1) em (2):
[( PA)/( PB)] = [( √{2 μC g dB})/( √{2 μC g dA})]
[( PA)/( PB)] = √{[( dB)/( dA)]}
Utilizando-se a fita métrica, medem-se as distâncias percorridas pelos garotos até sua imobilização e, por meio da expressão acima, determina-se a relação entre seus pesos.
Resposta: Foram utilizados o teorema da energia cinética (ou princípio de conservação da energia mecânica) e o princípio de conservação da quantidade de movimento.
Considere uma garrafa térmica fechada contendo uma certa quantidade de água inicialmente a 20oC. Elevando-se a garrafa a uma certa altura e baixando-a em seguida, suponha que toda a água sofra uma queda livre de 42 cm em seu interior. Este processo se repete 100 vezes por minuto. Supondo que toda a energia cinética se transforme em calor a cada movimento, determine o tempo necessário para ferver toda a água.
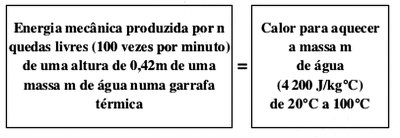
n = [( 4200 . (100 − 20))/ 10 . 0,42]
| n = 80000 quedas |
Para calcular o tempo ∆t para a fervura da água, vem:
| ∆t = 800 minutos |
Considere superpostas três barras idênticas de grafite com resistividade ρ = 1,0 ×10−4 Ωm, 15 cm de comprimento e seção quadrada com 2,0 em de lado. Inicialmente as três barras têm as suas extremidades em contato com a chapa ligada ao contato A. Em seguida, a barra do meio desliza sem atrito com velocidade constante v = 1,0 cm/s, movimentando igualmente o contato B, conforme a figura. Obtenha a expressão da resistência R medida entre A e B como função do tempo e esboce o seu gráfico.
Seja A a área da seção transversal:
A = (2,0 cm)2 = (2,0 . 10−2m)2 = 4,0 . 10−4 m2
Então a resistência R de cada barra é dada pela 2a Lei de Ohm:
R = 1,0 . 10−4 [( 15 . 10−2)/( 4,0 . 10−4)] (unidades SI)
| R = 3,75 . 10−2 Ω |
Para t = 0, as três barras superpostas são equivalentes a três resistores em paralelo (fig. 1)
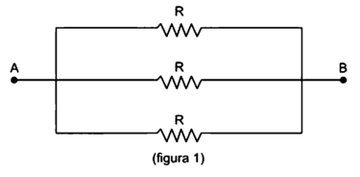
| R0 = 1,25 . 10−2 Ω |
A barra do meio desliza com velocidade constante V = 1,0 cm/s e percorre os 15 cm de comprimento num intervalo de tempo de 15 s.
Assim, para t = 15 s teremos a situação da figura (2):
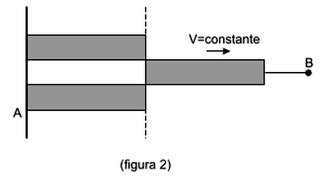
Essa situação é equivalente a:
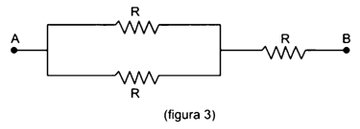
Rf = [( 3 ×3,75 . 10−2)/ 2] (Ω)
Como a barra do meio foi deslizada com velocidade escalar constante, podemos concluir que a variação da resistência equivalente obedece a uma função de 1o grau em t. Assim, temos o gráfico da figura 4.
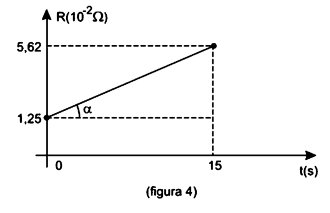
Do gráfico, obtemos o coeficiente angular da reta:
m = tanα = [( (5,62 − 1,25) . 10−2 Ω)/ 15s]
A equação dessa reta é a função procurada:
R = 1,25 . 10−2 + 0,29 . 10−2 t (unidades SI)
Na ausência da gravidade e no vácuo, encontram-se três esferas condutoras alinhadas, A, B e C, de mesmo raio e de massas respectivamente iguais a m, m e 2m. Inicialmente B e C encontram-se descarregadas e em repouso, e a esfera A, com carga elétrica Q, é lançada contra a intermediária B com uma certa velocidade v. Supondo que todos movimentos ocorram ao longo de uma mesma reta, que as massas sejam grandes o suficiente para se desprezar as forças coulombianas e ainda que todas as colisões sejam elásticas, determine a carga elétrica de cada esfera após todas as colisões possíveis.
Colisão entre A e B: há troca de velocidade (colisão frontal e perfeitamente elástica entre corpos de mesma massa).

A carga Q de A se divide em Q/2 para A e Q/2 para B (eletrização por contato entre esferas iguais).
Colisão entre B e C: A carga Q/2 de B se divide em Q/4 para B e Q/4 para C. Cálculo das velocidades de B e C após a colisão:
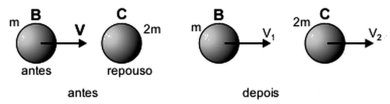
e = [( vel. rel. depois)/( vel. rel. antes)]
1 = [( v2 − v1)/ v] ⇒ v2 − v1 = v (1)
A esfera B volta após o choque com a esfera C e colide novamente com A. Entre A e B, ocorre eletrização por contato e suas cargas elétricas passam a ser:
[( [ Q/ 2] + [ Q/ 4])/ 2] = [ 3Q/ 8]
Assim, A e B ficam com cargas iguais a [ 3Q/ 8] e C fica com carga [ Q/ 4].
Pelo princípio de conservação das cargas elétricas, temos:
[ 3Q/ 8] + [ 3Q/ 8] + [ Q/ 4] = Q
Um sistema mecânico é formado por duas partículas de massas m conectadas por uma mola, de constante elástica k e comprimento natural 2 l0, e duas barras formando um ângulo fixo de 2 α, conforme a figura. As partículas podem se mover em movimento oscilatório, sem atrito, ao longo das barras, com a mola subindo e descendo sempre na horizontal. Determine a frequência angular da oscilação e a variação ∆l = l0 − l1, em que l1 é o comprimento da mola em sua posição de equilíbrio.
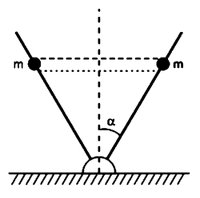
Cada partícula realiza um MHS na direção da barra.
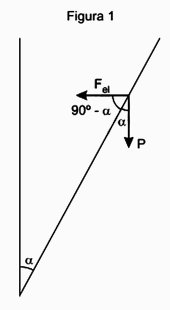
Aplicando o princípio fundamental da Dinâmica, temos:
k . ∆l. sen α+ m g cosα = m a (1)
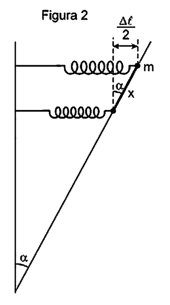
sen α = [( ∆l)/ 2x] ⇒ ∆l = 2x sen α
Logo: k . 2x sen α. sen α+ m g cosα = ma
a = [( 2k . sen2 α)/ m] . x + g cosα
com A e B constantes, e A = ω2.
A equação a = Ax + B é característica do MHS.
Na posição de equilíbrio, fazendo a = 0 na equação (1), vem:
| |∆l| = [( m g cotα)/ k] |
Obs.: Consideramos o comprimento natural da mola igual a l0.
No circuito da figura o capacitor encontra-se descarregado com a chave A aberta que, a seguir, é fechada no instante t1, sendo que o capacitor estará totalmente carregado no instante t2. Desprezando a resistência da bateria V, determine a corrente no circuito nos instantes t1 e t2.
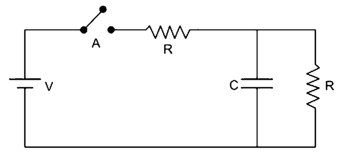
No instante t1, quando a chave é fechada, o capacitor entra em processo de carga. Nesse instante, atuará como um curto-circuito para o resistor que está associado em paralelo com ele, assim:
No instante t2, com o capacitor plenamente carregado, ele atua como circuito aberto, ou seja, não é percorrido por corrente elétrica, assim: