Índice Superior Vai para o próximo: Capítulo 20
Arquivos de Impressão: Capítulo 19 em Tamanho A4, Capítulo 19 em Tamanho A5.
Livro em Texto (txt).
Como Multiplicar a
Inteligência do Seu Bebê
mais suave revolução
Glenn Doman • Janet Doman

Capítulo 19
Como Podem Crianças Bem Novinhas Utilizar Matemática Instantânea?
Institutos para o Desenvolvimento do Potencial Humano
Institutes for the Achievment of Human Potential
19 Como Podem Crianças Bem Novinhas Utilizar Matemática Instantânea?
A pergunta não é: "Como podem crianças muito pequenas utilizar a matemática instantânea?" Mas sim: "Como é possível aos adultos que podem falar uma língua não serem capazes de utilizar a matemática instantânea?"
O problema é que em matemática nós misturamos o símbolo "5" com o fato
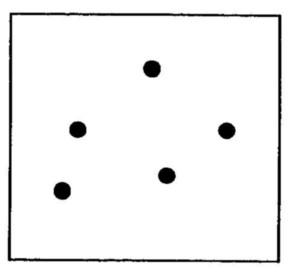
Quando o problema está na ordem de 5 ou

não é muito complicado porque o adulto é capaz de perceber o símbolo ou o fato sucessivamente de um

até mais ou menos 12
Com algum grau de confiabilidade.
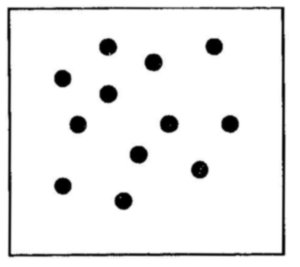
De 12

a mais ou menos 20

a confiabilidade, ainda que a do adulto mais esperto, começa a decrescer vertiginosamente.
De 20

em diante passa a ser adivinhação, e muitas vezes má adivinhação.
As crianças que já conhecem os símbolos, por exemplo 5, 7, 10, 13, mas que não conhecem os fatos

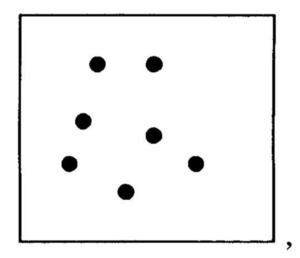
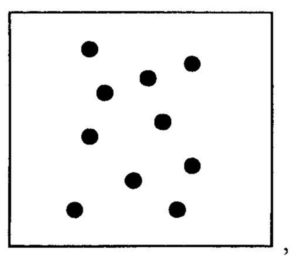
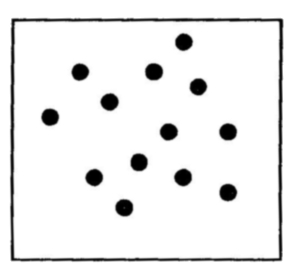
são incapazes de utilizar corretamente a matemática instantânea.
As pequeninas, porém, vêem as coisas como são enquanto nós, adultos, temos a tendência a ver as coisas como nós pensamos que elas devam ser.
Eu acho enlouquecedor que, enquanto eu entendo como crianças de dois anos utilizam a matemática instantânea, eu não possa fazer o mesmo. E a razão disso é que se você diz "setenta e nove" para mim, eu só consigo ver
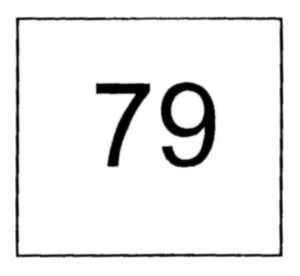
Eu não sou capaz de ver
Não é bem verdade que eu não consiga ver o cartão acima. Eu posso ver, mas não posso perceber.
As crianças bem pequenas podem.
Para que crianças bem pequenas percebam a verdade em um (1) que é realmente

precisamos simplesmente mostrar à criança o fato

e dizer: - Isso é chamado um.
Em seguida apresentamos o fato
e dizemos: - Isso é dois.
Depois dizemos: - Isso é três, mostrando à criança
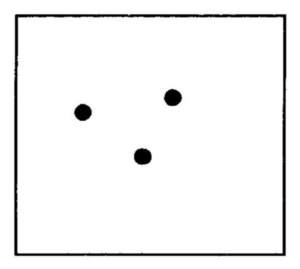
e assim por diante. Nós temos que apresentar cada cartão algumas vezes até que a criança possa perceber e reter a verdade.
A mente do adulto, ao encarar os fatos, é inclinada ao deslumbramento e muitos preferem acreditar que a criança que pode reconhecer de

até

é, de alguma forma, paranormal, e não que uma criança de dois anos possa desempenhar uma função de natureza intelectual que nós, adultos, não conseguimos.
A próxima desculpa à qual nos apegamos é a crença de que ela não está reconhecendo verdadeiramente o número, mas o padrão no qual ocorre.
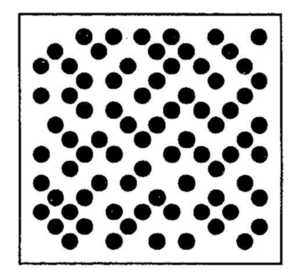
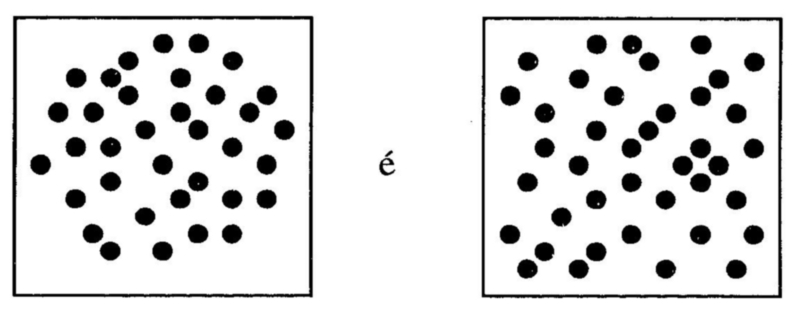
Qualquer bebê de um ano e que ainda não tenha sido iludido a reconhecer símbolos antes de poder reconhecer os fatos, pode dizer com um simples olhar que

ou de qualquer outra maneira que você queira apresentá-los, que os pontos totalizam o que chamamos - 27? Desculpem-nos, nós os enganamos - são de fato quarenta, e não 27!
Nós, adultos, só podemos ver isso se nos for apresentado o símbolo "40".
As crianças não se enganam, independentemente da forma com que os fatos são apresentados, e vêem somente a verdade, enquanto nós adultos temos que contar os pontos quando existe um padrão ou multiplicá-los se apresentados em forma de colunas. Por isso, se damos a informação assim,

resolvemos nosso problema contando os pontos enquanto a criança pequena pode ver a verdade de imediato.
Se apresentamos os fatos em forma de colunas

os adultos irão contar as linhas horizontais que são 8 e as verticais que são 5, e então usar uma fórmula aritmética que conhecemos como
ou em forma algébrica: 8x5 = 40.
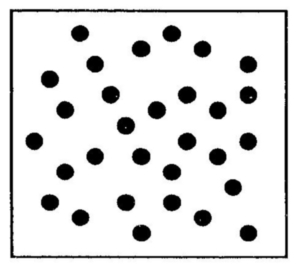
Este processo demorado nada tem a seu favor a não ser chegar a um resultado correto no final. Entretanto, ainda que chegue ao resultado correto, que percebemos como 40, nós não temos a menor idéia do que quarenta significa, exceto comparado a outras coisas como o número de dólares que eu recebo num dia, ou um mês mais dez dias. A criança vê a verdade
absoluta, ou seja, que
Nada mais ou nada menos.
Se tivermos que fazer a comparação usando meses, então é justo dizer que a criança que teve a oportunidade de perceber a verdade sabe que setembro, abril, junho e novembro têm
dias.
Portanto, se estivermos comparando o que chamamos 40 com um mês, estaremos nos referindo a
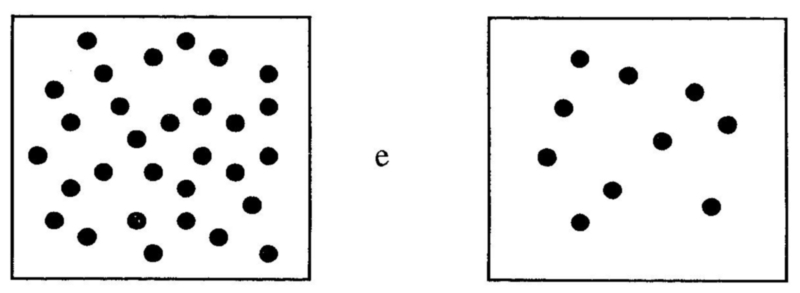
como qualquer criança pode muito bem ver.

















